Skip to contents

Univariate Poisson Cost Calculations

Source: vignettes/univariate_poisson.Rmd
univariate_poisson.Rmd

The purpose of this vignette is to present the calculations of the costs for the univariate Poisson distribution.

Each time step tt belongs to group kk whose time stamps are the set TkT_{k}. A group can have a multiplicative rate anomaly λk\lambda_{k} which is common for t∈Tkt \in T_{k}. Assuming the {} known rate rtr_{t} the data generating distribution gives for t∈Tkt \in T_{k}

P(yt|rt,λk)=λkytrtytexp(−rtλk)yt! P\left(y_t \left| r_t, \lambda_k\right.\right) = \frac{\lambda_{k}^{y_{t}} r_{t}^{y_{t}} \exp\left(-r_{t}\lambda_{k}\right)}{y_{t}!}

The cost is computed as twice the negative log likelhiood plus a penalty term β\beta giving

C(yt∈Tk|λk,rt∈Tk)=2λk∑t∈Tkrt−2log(λk)∑t∈Tkyt−2∑t∈Tkytlog(rt)+2∑t∈Tklog(yt!)+β C\left(y_{t \in T_{k}} \left| \lambda_k,r_{t \in T_{k}}\right.\right) = 2 \lambda_{k} \sum\limits_{t \in T_{k}} r_{t} - 2 \log\left(\lambda_{k}\right) \sum\limits_{t \in T_{k}} y_{t} - 2 \sum\limits_{t \in T_{k}} y_{t} \log\left(r_{t}\right) + 2 \sum\limits_{t \in T_{k}} \log\left( y_{t}! \right) + \beta

No Anomaly (Baseline)

In this case λk=1\lambda_{k}=1 and there is no penalty so

CB(yt∈Tk|rt∈Tk)=2∑t∈Tkrt−2∑t∈Tkytlog(rt)+2∑t∈Tklog(yt!) C_{B}\left(y_{t \in T_{k}} \left| r_{t \in T_{k}}\right.\right) = 2 \sum\limits_{t \in T_{k}} r_{t} - 2 \sum\limits_{t \in T_{k}} y_{t} \log\left(r_{t}\right) + 2 \sum\limits_{t \in T_{k}} \log\left( y_{t}! \right)

Anomaly in Rate

An estimate λ̂k\hat{\lambda}_{k} of λk\lambda_{k} can be selected to minimise the cost by taking λ̂k=∑t∈Tkyt∑t∈Tkrt \hat{\lambda}_{k} = \frac{ \sum\limits_{t \in T_{k}} y_{t} }{\sum\limits_{t \in T_{k}} r_{t}}

CA(yt∈Tk|λ̂k,rt∈Tk)=2∑t∈Tkyt−2log(λ̂k)∑t∈Tkyt−2∑t∈Tkytlog(rt)+2∑t∈Tklog(yt!)+β C_{A}\left(y_{t \in T_{k}} \left| \hat{\lambda}_k,r_{t \in T_{k}}\right.\right) = 2 \sum\limits_{t \in T_{k}} y_{t} - 2 \log\left(\hat{\lambda}_{k}\right) \sum\limits_{t \in T_{k}} y_{t} - 2 \sum\limits_{t \in T_{k}} y_{t} \log\left(r_{t}\right) + 2 \sum\limits_{t \in T_{k}} \log\left( y_{t}! \right) + \beta

An anomaly will be accepted whenever

CA(yt∈Tk|λ̂k,rt∈Tk)−CB(yt∈Tk|rt∈Tk)=2∑t∈Tkyt−2log(λ̂k)∑t∈Tkyt+β−2∑t∈Tkrt<0 C_{A}\left(y_{t \in T_{k}} \left| \hat{\lambda}_k,r_{t \in T_{k}}\right.\right) - C_{B}\left(y_{t \in T_{k}} \left| r_{t \in T_{k}}\right.\right) = 2 \sum\limits_{t \in T_{k}} y_{t} - 2 \log\left(\hat{\lambda}_{k}\right) \sum\limits_{t \in T_{k}} y_{t} + \beta - 2 \sum\limits_{t \in T_{k}} r_{t} <0

Rearranging this expression in terms of ∑t∈Tkrt\sum\limits_{t \in T_{k}} r_{t}, the expected number of counts if the period was not anomalous gives

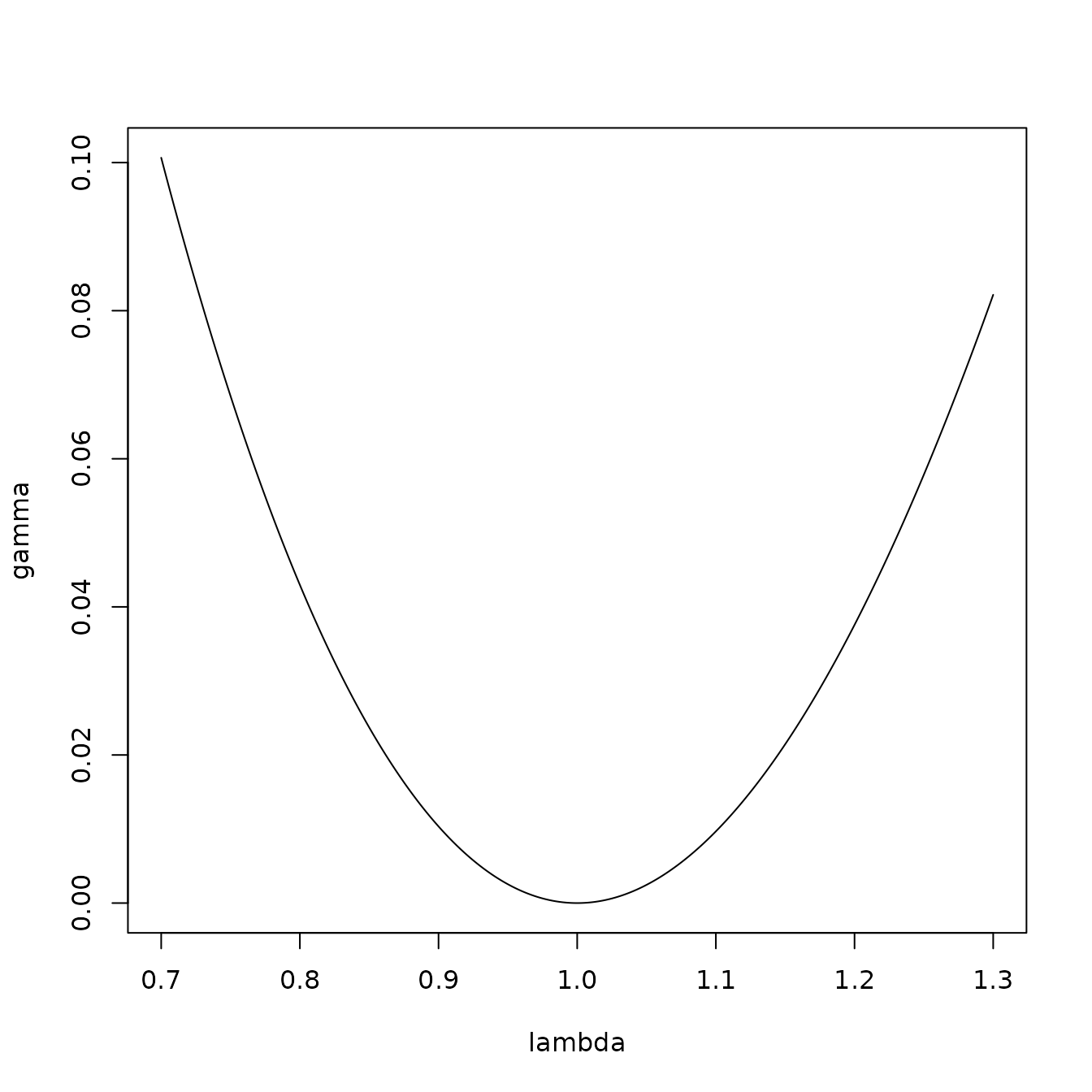
CA(yt∈Tk|λ̂k,rt∈Tk)−CB(yt∈Tk|rt∈Tk)=β−2(1−λ̂k+λ̂klog(λ̂k))∑t∈Tkrt C_{A}\left(y_{t \in T_{k}} \left| \hat{\lambda}_k,r_{t \in T_{k}}\right.\right) - C_{B}\left(y_{t \in T_{k}} \left| r_{t \in T_{k}}\right.\right) = \beta - 2 \left( 1 - \hat{\lambda}_{k} + \hat{\lambda}_{k}\log\left(\hat{\lambda}_{k}\right)\right) \sum\limits_{t \in T_{k}} r_{t}

This form suggests the selection of β\beta based on a minimum change in λ̂k\hat{\lambda}_{k} away from 1 causing at least a certain change from the expected number of counts. The figure below show γ=2(1−λ̂k+λ̂klog(λ̂k))\gamma = 2 \left( 1 - \hat{\lambda}_{k} + \hat{\lambda}_{k}\log\left(\hat{\lambda}_{k}\right)\right). Using this we could select gamma=0.01gamma=0.01 to ensure a change in in lambda of 10%, which combined with a desire to detect only changes of 50 units would result in β=0.5\beta = 0.5