Skip to contents

Regression Cost Calculations

Source: vignettes/regression_cost_calcs.Rmd
regression_cost_calcs.Rmd

The purpose of this vignette is to present the calculations for a peicewise linear regression where for each time step there are multiple independent observations.

In the follow variables identified by Greek letters are considered unknown.

Linear regression

At time step tt the vector of iid observations 𝐲t={yt,1,…,yt,p}\mathbf{y}_{t}=\left\{y_{t,1},\ldots,y_{t,p}\right\} is explained by the design matrix 𝐗t\mathbf{X}_{t} and modelled as a multivariate Gaussian distribution. Consider known, β€˜β€™background’’, parameters 𝐦t\mathbf{m}_{t} and precision matrix 𝐒t=𝐔′𝐔\mathbf{S}_{t} = \mathbf{U}^{\prime}\mathbf{U} deviation from which are modelled by ΞΈ\theta and Ξ›\Lambda through the likelihood

L(𝐲t|ΞΈ,Ξ»)=(2Ο€)βˆ’p/2det(𝐒t)1/2det(Ξ›)1/2exp(βˆ’12(𝐲tβˆ’π—t𝐦tβˆ’π—tΞΈ)′𝐔′Λ𝐔(𝐲tβˆ’π—t𝐦tβˆ’π—tΞΈ)) L\left(\mathbf{y}_{t} \left| \theta,\lambda\right.\right) = \left(2\pi\right)^{-p/2} \det\left(\mathbf{S}_{t}\right)^{1/2} \det\left(\Lambda\right)^{1/2} \exp\left(-\frac{1}{2}\left( \mathbf{y}_{t} - \mathbf{X}_{t} \mathbf{m}_{t} - \mathbf{X}_{t} \theta\right)^{\prime} \mathbf{U}^{\prime} \Lambda \mathbf{U} \left( \mathbf{y}_{t} - \mathbf{X}_{t} \mathbf{m}_{t} - \mathbf{X}_{t} \theta\right) \right)

Pre whitening the known values such that 𝐲̂t=𝐔t(𝐲tβˆ’π—t𝐦t)\hat{\mathbf{y}}_{t} = \mathbf{U}_{t} \left(\mathbf{y}_{t} - \mathbf{X}_{t} \mathbf{m}_{t}\right) and 𝐗̂t=𝐔t𝐗t\hat{\mathbf{X}}_{t} = \mathbf{U}_{t} \mathbf{X}_{t} gives

L(𝐲t|ΞΈ,Ξ›)=(2Ο€)βˆ’p/2det(𝐒t)1/2det(Ξ›)1/2exp(βˆ’12(𝐲̂tβˆ’π—Μ‚tΞΈ)β€²Ξ›(𝐲̂tβˆ’π—Μ‚tΞΈ)) L\left(\mathbf{y}_{t} \left| \theta,\Lambda\right.\right) = \left(2\pi\right)^{-p/2} \det\left(\mathbf{S}_{t}\right)^{1/2} \det\left(\Lambda\right)^{1/2} \exp\left(-\frac{1}{2}\left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta\right)^{\prime} \Lambda \left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta\right) \right)

Grouping the known values into Kt=plog(2Ο€)βˆ’log(det𝐒t)K_{t} = p\log\left(2\pi\right) - \log\left(\det{\mathbf{S}_{t}}\right) the log likelihood is l(𝐲t|ΞΈ,Ξ›)=βˆ’12Kt+12log(det(Ξ›))βˆ’12(𝐲̂tβˆ’π—Μ‚tΞΈ)β€²Ξ›(𝐲̂tβˆ’π—Μ‚tΞΈ) l\left(\mathbf{y}_{t} \left| \theta,\Lambda \right.\right) = -\frac{1}{2}K_{t} + \frac{1}{2}\log\left( \det\left(\Lambda\right)\right) -\frac{1}{2}\left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta\right)^{\prime} \Lambda \left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta\right)

Suppose an anomaly with common parameters occurs of nkn_{k} consecuative time steps in the set TkT_{k}. The log-likelihood of 𝐲t∈Tk\mathbf{y}_{t \in T_{k}} is l(𝐲t∈Tk|ΞΈk,Ξ›k)=βˆ’12βˆ‘t∈TkKt+nk2log(det(Ξ›))βˆ’12βˆ‘t∈Tk(𝐲̂tβˆ’π—Μ‚tΞΈk)β€²Ξ›k(𝐲̂tβˆ’π—Μ‚tΞΈk) l\left(\mathbf{y}_{t \in T_{k}} \left| \theta_{k},\Lambda_{k} \right.\right) = -\frac{1}{2}\sum_{t \in T_{k}}K_{t} + \frac{n_{k}}{2}\log\left( \det\left(\Lambda\right)\right) -\frac{1}{2}\sum_{t \in T_{k}}\left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right)^{\prime} \Lambda_{k} \left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right)

with the cost being twice the negative log likelihood plus a penalty Ξ²\beta giving

C(𝐲t∈Tk|ΞΈk,Ξ›k)=βˆ‘t∈TkKtβˆ’nklog(det(Ξ›))+βˆ‘t∈Tk(𝐲̂tβˆ’π—Μ‚tΞΈk)β€²Ξ›k(𝐲̂tβˆ’π—Μ‚tΞΈk)+Ξ² C\left(\mathbf{y}_{t \in T_{k}} \left| \theta_{k}, \Lambda_{k} \right.\right) = \sum_{t \in T_{k}}K_{t} - n_{k}\log\left( \det\left(\Lambda\right)\right) +\sum_{t \in T_{k}}\left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right)^{\prime} \Lambda_{k} \left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right) + \beta

Sufficent statistics

Computation is greatly aided by being able to keep adequate sufficent statistics. Expanding the summation in the cost gives βˆ‘t∈Tk(𝐲̂tβˆ’π—Μ‚tΞΈk)β€²Ξ›k(𝐲̂tβˆ’π—Μ‚tΞΈk)=βˆ‘t∈Tk(𝐲̂t′Λ𝐲̂t+ΞΈk′𝐗̂t′Λ𝐗̂tΞΈkβˆ’2ΞΈk′𝐗̂t′Λ𝐲̂t) \sum_{t \in T_{k}}\left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right)^{\prime} \Lambda_{k} \left( \hat{\mathbf{y}}_{t} - \hat{\mathbf{X}}_{t} \theta_{k}\right) = \sum_{t \in T_{k}} \left( \hat{\mathbf{y}}^{\prime}_{t} \Lambda \hat{\mathbf{y}}_{t} + \theta^{\prime}_{k}\hat{\mathbf{X}}^{\prime}_{t} \Lambda \hat{\mathbf{X}}_{t} \theta_{k} - 2 \theta^{\prime}_{k} \hat{\mathbf{X}}^{\prime}_{t}\Lambda \hat{\mathbf{y}}_{t} \right) βˆ‘t∈Tk(tr(𝐲̂t𝐲̂tβ€²Ξ›)+ΞΈk′𝐗̂t′Λ𝐗̂tΞΈkβˆ’2ΞΈk′𝐗̂t′Λ𝐲̂t) \sum_{t \in T_{k}} \left( \mathrm{tr}\left( \hat{\mathbf{y}}_{t}\hat{\mathbf{y}}^{\prime}_{t} \Lambda \right) + \theta^{\prime}_{k}\hat{\mathbf{X}}^{\prime}_{t} \Lambda \hat{\mathbf{X}}_{t} \theta_{k} - 2 \theta^{\prime}_{k} \hat{\mathbf{X}}^{\prime}_{t}\Lambda \hat{\mathbf{y}}_{t} \right)

Baseline: No Anomaly

Here ΞΈk=𝟎\theta_{k}=\mathbf{0}, Ξ›k\Lambda_{k} is an identify matrix and there is no penalty so Ξ²=0\beta = 0. The resulting csot is CB(𝐲t∈Tk|ΞΈk,Ξ›k)=βˆ‘t∈TkKt+βˆ‘t∈Tk𝐲̂t′𝐲̂t C_{B}\left(\mathbf{y}_{t \in T_{k}} \left| \theta_{k}, \Lambda_{k} \right.\right) = \sum_{t \in T_{k}} K_{t} + \sum_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \hat{\mathbf{y}}_{t}

Collective Anomalies

Anomaly in Regression parameters

There is no change in variance so Ξ›k\Lambda_{k} is an identify matrix. The estimate ΞΈΜ‚k\hat{\theta}_{k} of ΞΈk\theta_{k} can be selected to minimise the cost by taking

ΞΈΜ‚k=(βˆ‘t∈Tk𝐗̂t′𝐗̂t)βˆ’1(βˆ‘t∈Tk𝐗̂t′𝐲̂t) \hat{\theta}_{k} = \left( \sum\limits_{t \in T_k} \hat{\mathbf{X}}_{t}^{\prime} \hat{\mathbf{X}}_{t} \right)^{-1} \left( \sum\limits_{t \in T_k} \hat{\mathbf{X}}_{t}^{\prime} \hat{\mathbf{y}}_{t} \right)

CC(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+(βˆ‘t∈Tk𝐲̂t′𝐒tβˆ’1𝐲̂t)βˆ’(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)β€²(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐗t)βˆ’1(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)+Ξ² C_{C}\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} + \left( \sum_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) - \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right)^{\prime} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \right)^{-1} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) +\beta

Anomaly in Variance

These is no mean anomaly in the regression parameters so ΞΈk=0\theta_{k}=0. The estimate of Οƒk\sigma_{k} therfore changes to

ΟƒΜ‚k=1nkβˆ‘t∈Tk𝐲̂t′𝐒tβˆ’1𝐲̂t \hat{\sigma}_{k} = \frac{1}{n_{k}} \sum\limits_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t}

while the cost is CC(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+nklog(ΟƒΜ‚k)+nk+Ξ² C_{C}\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} +n_{k} \log\left(\hat{\sigma}_{k}\right) +n_{k} +\beta

Anomaly in regression parameters and variance

Since βˆ‘t∈Tk(𝐲̂tβˆ’π—tΞΈk)′𝐒tβˆ’1(𝐲̂tβˆ’π—tΞΈk)=βˆ‘t∈Tk(𝐲̂t′𝐒tβˆ’1𝐲̂tβˆ’2ΞΈk′𝐗t′𝐒tβˆ’1𝐲̂t+ΞΈk′𝐗t′𝐒tβˆ’1𝐗tΞΈk) \sum_{t \in T_{k}} \left( \hat{\mathbf{y}}_{t} - \mathbf{X}_{t} \theta_{k}\right)^{\prime} \mathbf{S}_{t}^{-1} \left( \hat{\mathbf{y}}_{t} - \mathbf{X}_{t} \theta_{k}\right) = \sum_{t \in T_{k}} \left( \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} - 2 \theta_{k}^{\prime}\mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1} \hat{\mathbf{y}}_{t} + \theta_{k}^{\prime}\mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \theta_{k} \right)

The estimate ΞΈΜ‚k\hat{\theta}_{k} of ΞΈk\theta_{k} can be selected to minimise the cost by taking ΞΈΜ‚k=(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐗t)βˆ’1(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t) \hat{\theta}_{k} = \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \right)^{-1} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right)

Subsitution of this result into the cost gives ΟƒΜ‚k=1nkβˆ‘t∈Tk(𝐲̂t′𝐒tβˆ’1𝐲̂tβˆ’2ΞΈΜ‚k′𝐗t′𝐒tβˆ’1𝐲̂t+ΞΈΜ‚k′𝐗t′𝐒tβˆ’1𝐗tΞΈΜ‚k) \hat{\sigma}_{k} = \frac{1}{n_{k}} \sum_{t \in T_{k}} \left( \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} - 2 \hat{\theta}_{k}^{\prime}\mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1} \hat{\mathbf{y}}_{t} + \hat{\theta}_{k}^{\prime}\mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \hat{\theta}_{k} \right) which simplifies to ΟƒΜ‚k=1nk[(βˆ‘t∈Tk𝐲̂t′𝐒tβˆ’1𝐲̂t)βˆ’(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)β€²(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐗t)βˆ’1(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)] \hat{\sigma}_{k} = \frac{1}{n_{k}} \left[ \left( \sum_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) - \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right)^{\prime} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \right)^{-1} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) \right]

The cost is given by CC(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+nklog(ΟƒΜ‚k)+nk+Ξ² C_{C}\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} +n_{k} \log\left(\hat{\sigma}_{k}\right) +n_{k} +\beta

Anomaly in Regression parameters

There is no change in variance so Οƒk=1\sigma_{k}=1. The estimate of ΞΈΜ‚k\hat{\theta}_{k} is unchanged which gives a cost of

CC(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+(βˆ‘t∈Tk𝐲̂t′𝐒tβˆ’1𝐲̂t)βˆ’(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)β€²(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐗t)βˆ’1(βˆ‘t∈Tk𝐗t′𝐒tβˆ’1𝐲̂t)+Ξ² C_{C}\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} + \left( \sum_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) - \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right)^{\prime} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\mathbf{X}_{t} \right)^{-1} \left( \sum\limits_{t \in T_k} \mathbf{X}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t} \right) +\beta

Anomaly in Variance

These is no mean anomaly in the regression parameters so ΞΈk=0\theta_{k}=0. The estimate of Οƒk\sigma_{k} therfore changes to

ΟƒΜ‚k=1nkβˆ‘t∈Tk𝐲̂t′𝐒tβˆ’1𝐲̂t \hat{\sigma}_{k} = \frac{1}{n_{k}} \sum\limits_{t \in T_{k}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t}

while the cost is CC(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+nklog(ΟƒΜ‚k)+nk+Ξ² C_{C}\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} +n_{k} \log\left(\hat{\sigma}_{k}\right) +n_{k} +\beta

Point anomaly

A point anomaly occurs at a single time instance and is represented as a variance anomaly. Naively the cost could be computed using the formulea for a variance anomaly as Cp(𝐲t|Οƒt)=Kt+ntlog(ΟƒΜ‚t)+nt+Ξ² C_{p}\left(\mathbf{y}_{t}\left| \sigma_{t}\right.\right) = K_{t} + n_{t} \log\left( \hat{\sigma}_{t} \right) + n_{t} + \beta with ΟƒΜ‚t=1nt𝐲̂t′𝐒tβˆ’1𝐲̂t \hat{\sigma}_{t} = \frac{1}{n_{t}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t}

Relating this to the background cost we see that point anomalies may be accepted in the capa search when f(ΟƒΜ‚t,Ξ³,Ξ²)=Cp(yt|ΞΌt,Οƒt)βˆ’CB(yt|ΞΌt,Οƒt)=ntlog(ΟƒΜ‚t)+nt+Ξ²βˆ’ntΟƒΜ‚t<0 f\left(\hat{\sigma}_{t},\gamma,\beta\right) = C_{p}\left(y_{t}\left| \mu_{t},\sigma_{t}\right.\right) - C_{B}\left(y_{t}\left| \mu_{t},\sigma_{t}\right.\right) = n_{t} \log \left( \hat{\sigma}_{t} \right) + n_{t} + \beta - n_{t} \hat{\sigma}_{t} < 0

The following plot shows log(ΟƒΜ‚t)+1βˆ’ΟƒΜ‚t\log \left( \hat{\sigma}_{t} \right) + 1 - \hat{\sigma}_{t} which indicates that point anomalies may be declared for both outlying and inlying data.

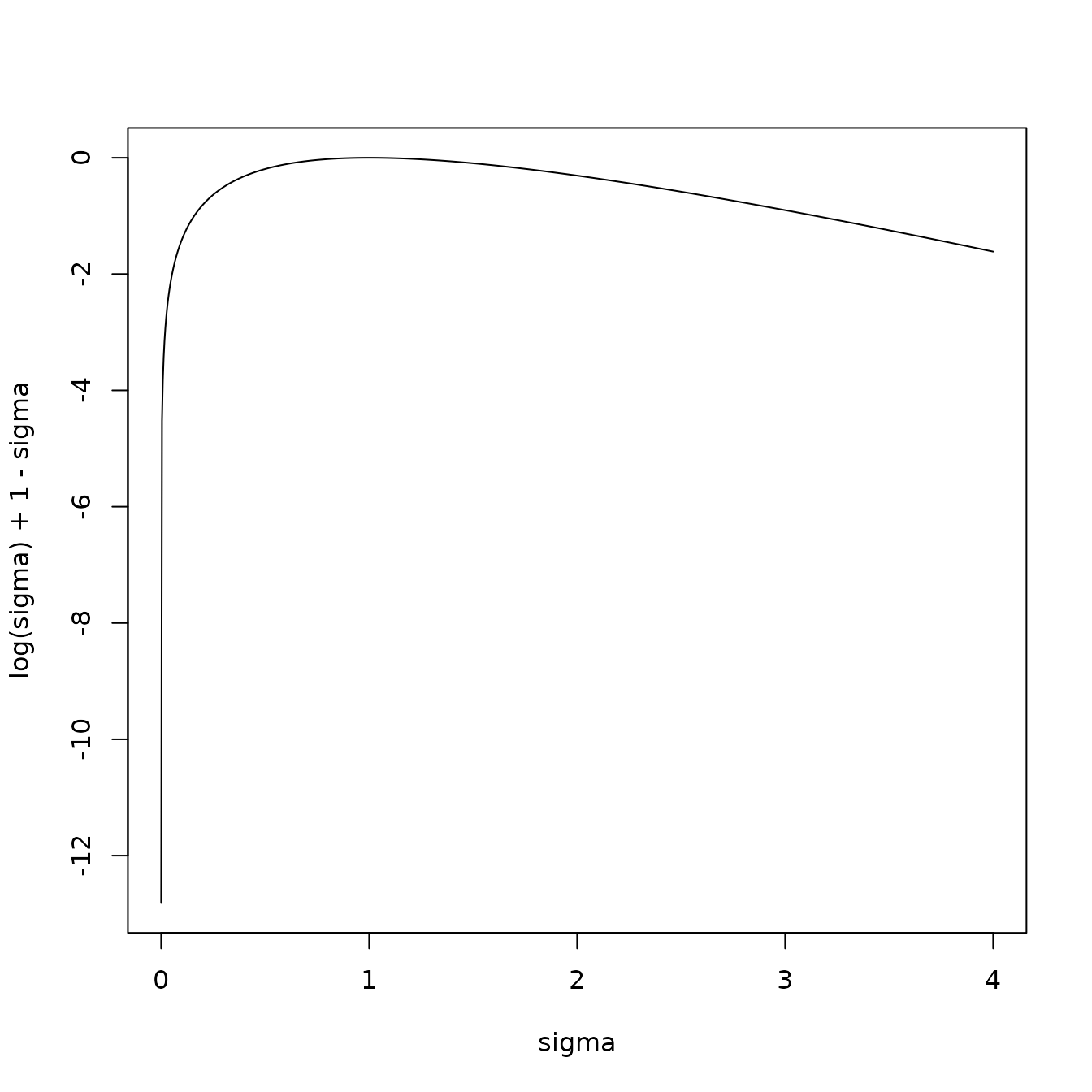
In the case of nt=1n_{t}=1 Fisch et al.Β control this by modifying the cost of a point anomaly so it is expressed as Cp(yt|Οƒt,𝐗t)=log(exp(βˆ’Ξ²)+ΟƒΜ‚t)+Kt+1+Ξ² C_{p}\left(y_{t}\left| \sigma_{t}, \mathbf{X}_{t}\right.\right) = \log\left(\exp\left(-\beta\right) + \hat{\sigma}_{t} \right) + K_{t} + 1 + \beta

This has the effect of allowing only outlier anomalies, something that can be much more easily acheived by taking

ΟƒΜ‚t=max(1,1nt𝐲̂t′𝐒tβˆ’1𝐲̂t) \hat{\sigma}_{t} = \max\left(1,\frac{1}{n_{t}} \hat{\mathbf{y}}_{t}^{\prime} \mathbf{S}_{t}^{-1}\hat{\mathbf{y}}_{t}\right)

giving the cost as

C(𝐲t∈Tk|ΞΌt,mk,Οƒk,sk)=βˆ‘t∈TkKt+nklog(ΟƒΜ‚k)+1ΟƒΜ‚kβˆ‘t∈Tk(𝐲̂t𝐒tβˆ’1𝐲̂t)+Ξ² C\left(\mathbf{y}_{t \in T_{k}} \left| \mu_t,m_k,\sigma_k,s_k\right.\right) = \sum_{t \in T_{k}} K_{t} +n_{k} \log\left(\hat{\sigma}_{k}\right) +\frac{1}{\hat{\sigma}_{k}}\sum_{t \in T_{k}} \left( \hat{\mathbf{y}}_{t} \mathbf{S}_{t}^{-1} \hat{\mathbf{y}}_{t} \right) +\beta